V tomto příspěvku je popsáno použití Řešitele. Je vysvětlené na jednoduchém příkladě, nicméně tuto funkcionalitu je možné používat i pro velmi sofistikované úlohy.
Uvedený příklad je inspirován jakýmisi skripty pro Operační výzkum, ale už nevím kterými :)
Co má firma vyrábět, aby maximalizovala tržby?
Než s ním budu pracovat, potřebuji si jej zprovoznit (pokud jsem ho ještě nepoužíval) a připravit si tabulku, se kterou budu pracovat.
Kliknu na tlačítko Office vlevo nahoře
Kliknu Možnosti aplikace Excel
Doplňky
V seznamu vyberu Řešitel
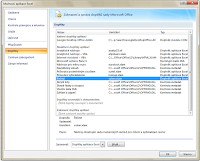
Kliknu na Přejít...
V navazujícím dialogu vyberu Řešitel
Případně potvrdím instalaci a nechám ji proběhnout
Že je vše OK poznám podle toho, že ve volbě Data mě vpravo přibude karta Řešitel.
A to je všechno. Hotový příklad je tady:
https://www.dropbox.com/s/y2l5v3xw99idcwd/resitel.xls
Uvedený příklad je inspirován jakýmisi skripty pro Operační výzkum, ale už nevím kterými :)
Příklad
Potřebuji vypočítat tento příklad:- Firma vyrábí hračky – autíčka a vláčky. K výrobě potřebuje pouze dřevo a plastová kolečka.
- Na jedno autíčko spotřebuje 4 kolečka a 0,8 metru dřeva.
- Na jeden vláček spotřebuje 6 koleček a 0,4 metru dřeva.
- Na jednom vláčku utrží 180 Kč a na jednom autíčku 120 Kč.
- Pro příští týden má k dispozici 1000 koleček a 200 metrů dřevěného materiálu.
Co má firma vyrábět, aby maximalizovala tržby?
Návod
Použiji funkcionalitu (nechci používat slovo funkce, protože z hlediska logiky Excelu to není funkce) Řešitel, v anglických verzích Solver.Než s ním budu pracovat, potřebuji si jej zprovoznit (pokud jsem ho ještě nepoužíval) a připravit si tabulku, se kterou budu pracovat.
Zprovoznění Řešitele
Popisuji Excel 2007, ale v dalších verzích je to plus minus podobné.Kliknu na tlačítko Office vlevo nahoře
Kliknu Možnosti aplikace Excel
Doplňky
V seznamu vyberu Řešitel

Kliknu na Přejít...
V navazujícím dialogu vyberu Řešitel
Případně potvrdím instalaci a nechám ji proběhnout
Že je vše OK poznám podle toho, že ve volbě Data mě vpravo přibude karta Řešitel.
Řešení úlohy
Připravím si takovouto tabulku:
- Ve sloupci A mam vypsané suroviny, jichž mám omezené množství. Jejich množství nakonec omezí počet výrobků, které mohu vyprodukovat.
- Ve sloupečcích B a C jsou pak jejich množství, které chci použít na jednotlivé výrobky.
- Do sloupce E napíšu, kolik maximálně mohu těchto surovin použít.
- Logicky bude například platit, že počet koleček použitých na vláčky krát počet vláčků plus počet koleček použitých na autíčka krát počet autíček musí být nakonec menší než počet koleček, které mám k dispozici. To samé s dřevem. Mohl bych po jednotlivých buňkách násobit, šikovnější je ale použit funkci SOUČIN.SKALÁRNÍ / SUMPRODUCT.
- V pátém řádku mám napsáno, kolik utržím za jednotlivé produkty, v D4 je pak součet - a právě tuto buňku, celkové tržby, chci maximalizovat.
- Hodnoty v řádku 5, stejně jako hodnoty ve sloupečku D, chci zjistit - dozvím se, kolik čeho mám vyrábět.
Použití Řešitele
- Otevřu řešitele a takto ho nakonfiguruji:
- Nastavit buňku
Vyberu D4. V této buňce mám hodnotu, u které chci dosáhnout co největší hodnotu - jsou v ní celkové tržby. - Rovno:
Vyberu maximalizovat - jde o tržby. Alternativně je možné minimalizovat i cílovat na určitou hodnotu. - Měněné buňky:
Vyberu B5 a C5. Excel bude tyto buňky tak dlouho měnit, dokud nedosáhne nejvyšších možných tržeb.
Omezující podmínky
Pomocí "Přidat" nastavím omezení, která se při optimalizaci nesmí překročit.
B5 a C5 musí být celá čisla - protože chci vyrábět hračky celé
B5 a C5 musí být kladné - protože nemohu vyrábět záporná množství výrobků
Buńky ve sloupečku D musí být menší než odpovídající buňky ve sloupečku E - protože materiál spotřebovaný celkem musí být menší než ten, co mám k dispozici - Kliknu na Řešit a Excel spočítá optimální kombinaci vyrobených hraček.
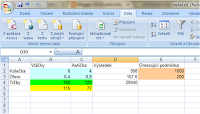
- V našem případě asi doplní do buněk B5 a C5 hodnoty 115 a 77 - největší tržby tedy budu mít při výrobě 115 vláčků a 77 autíček.
- Do sloupečku D dostanu počty spotřebovaného materiálu a skutečné tržby, kterých dosáhnu.

A to je všechno. Hotový příklad je tady:
https://www.dropbox.com/s/y2l5v3xw99idcwd/resitel.xls








Tak jsem to zkusil, a vyšla mi lepší maximalizace zisku, jak autorovi článku.
OdpovědětVymazatZkusil jsem na to přijít proč a najednou koukám - existuje velké množství řešení, které splňují tuto podmínku a současně jsou lepším řešením než autorovým. Proto řešitel má s tímto problém a výsledek je pokaždé jiný - záleží na startovacích hodnotách.
Pro tento příklad se měly zvolit lepší vstupní hodnoty tak, aby řešení bylo jednoznačné.
Ano, je to tak.
OdpovědětVymazatSprávný přístup by byl zkoušet různé vstupní hodnoty.
Řešitel má totiž tu vlastnost, že vezme hodnoty, které jste zadali jako vstupní, a upravuje je, dokud se zlepšuje hodnota maximalizační funkce.
Jenže někdy se stane, že Řešitel narazí na lokální maximum funkce (které ale není současně globálním maximem) a chybně ho jako globální maximum zhodnotí.
Myslím že se to dá možná vylepšit volbou jiného způsobu řešení (což Řešitel umožňuje) přesně ty algoritmy neznám...